Here are the Code examples of this chapter. These pages are currently being updated over time (adding pictures, captions, and possibly further examples). Visit again soon for updates. Of course, the best way to use this page is together with the book for getting the explanations.
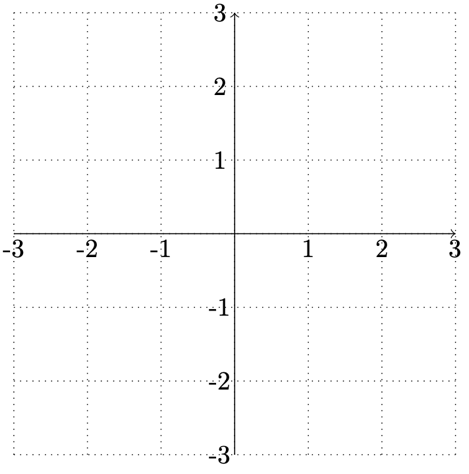
Figure 10.1 – A grid with axis labels
\documentclass[tikz,border=10pt]{standalone}
\begin{document}
\begin{tikzpicture}
\draw[thin,dotted] (-3,-3) grid (3,3);
\draw[->] (-3,0) -- (3,0);
\draw[->] (0,-3) -- (0,3);
\foreach \i in {-3,-2,-1,1,2,3} {
\node at (\i,-0.2) {\i};
\node at (-0.2,\i) {\i};
}
\end{tikzpicture}
\end{document}
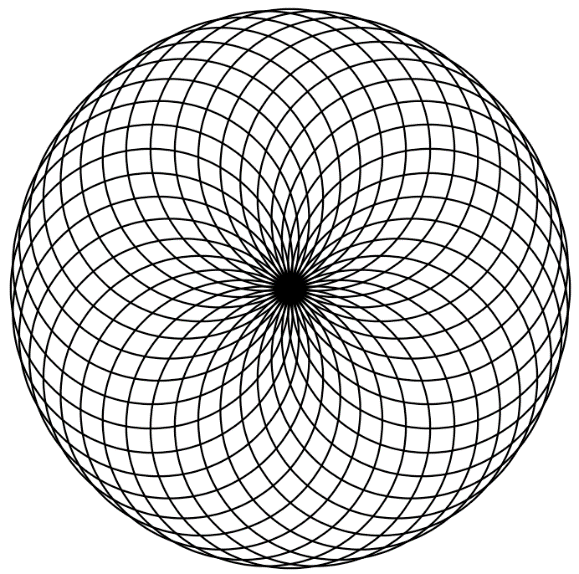
Figure 10.2 – Rotated circles
\documentclass[tikz,border=10pt]{standalone}
\begin{document}
\begin{tikzpicture}
\draw \foreach \i in {10,20,...,360} {(\i:1) circle (1)};
\end{tikzpicture}
\end{document}

Figure 10.3 – Filled intersecting circles
\documentclass[tikz,border=10pt]{standalone}
\begin{document}
\begin{tikzpicture}
\filldraw[even odd rule] \foreach \i in {10,20,...,360} {(\i:1) circle (1)};
\end{tikzpicture}
\end{document}
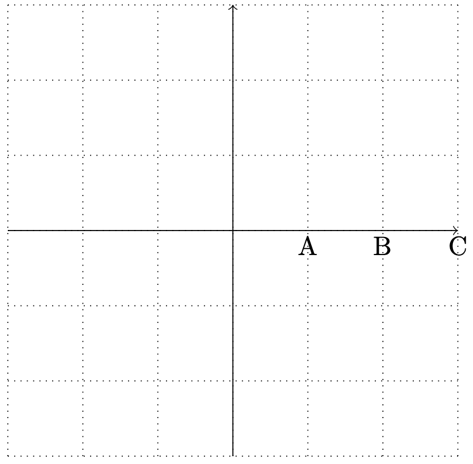
Figure 10.4 – Alphanumeric labels
\documentclass[tikz,border=10pt]{standalone}
\begin{document}
\begin{tikzpicture}
\draw[thin,dotted] (-3,-3) grid (3,3);
\draw[->] (-3,0) -- (3,0);
\draw[->] (0,-3) -- (0,3);
\foreach \i/\j in {A/1,B/2,C/3} \node at (\j,-0.2) {\i};
\end{tikzpicture}
\end{document}
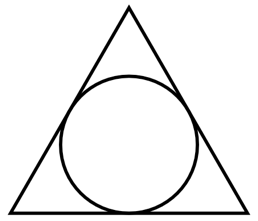
Figure 10.5 – Triangle with an inscribed circle
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\coordinate (A) at (1,2);
\coordinate (B) at ($(A)+(1,0)$);
\coordinate (C) at ($(A)+(60:1)$);
\draw (A) -- (B) -- (C) --cycle;
\draw ($(A)!0.5!(B)+(0,{sqrt(3)/6})$) circle({sqrt(3)/6});
\end{tikzpicture}
\end{document}
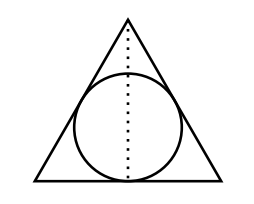
Figure 10.6 – Projection on a line
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\coordinate (A) at (1,2);
\coordinate (B) at ($(A)+(1,0)$);
\coordinate (C) at ($(A)+(60:1)$);
\draw (A) -- (B) -- (C) --cycle;
\draw ($(A)!0.5!(B)+(0,{sqrt(3)/6})$) circle({sqrt(3)/6});
\draw[densely dotted] (C) -- ($(A)!(C)!(B)$);
\end{tikzpicture}
\end{document}
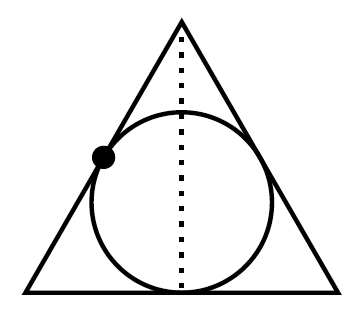
Figure 10.7 – Using a partway modifier with an angle
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\coordinate (A) at (1,2);
\coordinate (B) at ($(A)+(1,0)$);
\coordinate (C) at ($(A)+(60:1)$);
\draw (A) -- (B) -- (C) --cycle;
\draw ($(A)!0.5!(B)+(0,{sqrt(3)/6})$) circle({sqrt(3)/6});
\draw[densely dotted] (C) -- ($(A)!(C)!(B)$);
\filldraw ($(A)!0.5!60:(B)$) circle (0.03);
\end{tikzpicture}
\end{document}

Figure 10.8 – A spiral of circles
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\foreach \i in {0,0.025,...,1}
\draw ($(0,0)!\i!\i*360:(1,0)$) circle(0.08*\i);
\end{tikzpicture}
\end{document}

Figure 10.9 – A spiral of balls
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\foreach \i in {0,0.025,...,6}
\draw[shading=ball] ($(0,0)!\i!\i*360:(1,0)$) circle(0.08*\i);
\end{tikzpicture}
\end{document}
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\foreach \i [evaluate=\i as \j using 40*\i] in {0,0.05,...,2}
\fill[fill=black!60!blue!\j!white] ($(0,0)!\i!\i*180:(1,0)$) -- ($(0,0)!\i+0.05!\i*180+9:(1,0)$) -- (0,0);
\end{tikzpicture}
\end{document}

Figure 10.10 – A colored segmented spiral
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{calc}
\begin{document}
\begin{tikzpicture}
\foreach \i [remember=\i as \j (initially 6),
evaluate=\i as \c using 20*\i] in {5.95,5.9,...,0}
\fill[fill=black!60!blue!\c!white]
($(0,0)!\i!\i*180:(1,0)$) --
($(0,0)!\j!\j*180:(1,0)$) -- (0,0);
\end{tikzpicture}
\end{document}
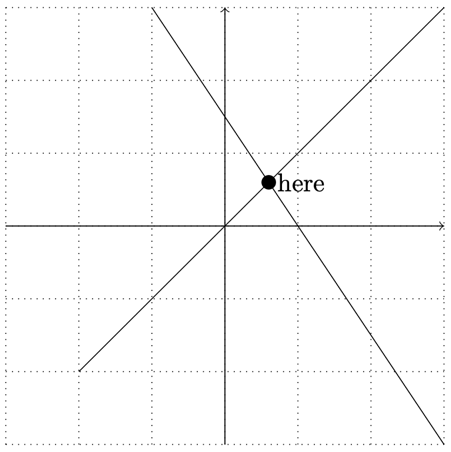
Figure 10.11 – A point at the intersection of two lines
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{intersections}
\begin{document}
\begin{tikzpicture}
\draw[thin,dotted] (-3,-3) grid (3,3);
\draw[->] (-3,0) -- (3,0);
\draw[->] (0,-3) -- (0,3);
\draw[name path = l1] (-2,-2) -- (3,3);
\draw[name path = l2] (-1,3) -- (3,-3);
\fill[name intersections = {of = l1 and l2}]
(intersection-1) circle(1mm) node[right] {here};
\end{tikzpicture}
\end{document}

Figure 10.12 – A filled triangle path with intersecting circles
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{intersections}
\begin{document}
\begin{tikzpicture}
\fill[name path=triangle, orange]
(90:2) -- (210:2) -- (330:2) -- cycle
(90:1) -- (330:1) -- (210:1) -- cycle;
\draw[name path=circle, dashed, gray]
circle(1.5) circle(0.65);
\end{tikzpicture}
\end{document}
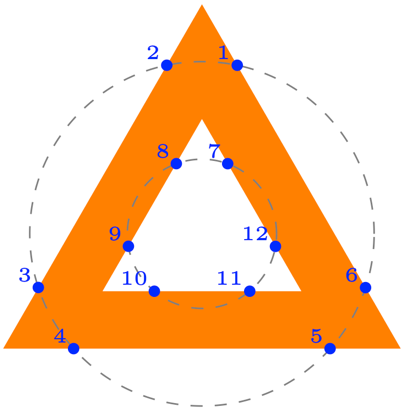
Figure 10.13 – Intersections of circles and triangles
\documentclass[tikz,border=10pt]{standalone}
\usetikzlibrary{intersections}
\begin{document}
\begin{tikzpicture}
\fill[name path=triangle, orange]
(90:2) -- (210:2) -- (330:2) -- cycle
(90:1) -- (330:1) -- (210:1) -- cycle;
\draw[name path=circle, dashed, gray]
circle(1.5) circle(0.65);
\fill[blue,
name intersections = {of = triangle and circle,
total=\max, name=c, sort by = circle}]
\foreach \i in {1,...,\max} {
(c-\i) circle(0.5mm)
node[above left=0.5mm,font=\tiny, inner sep=0]{\i}};
\end{tikzpicture}
\end{document}
Please rate (and possibly review) the book on Amazon if you got it there, your feedback means much to me and helps to get an extended second edition!
Go to next chapter.